
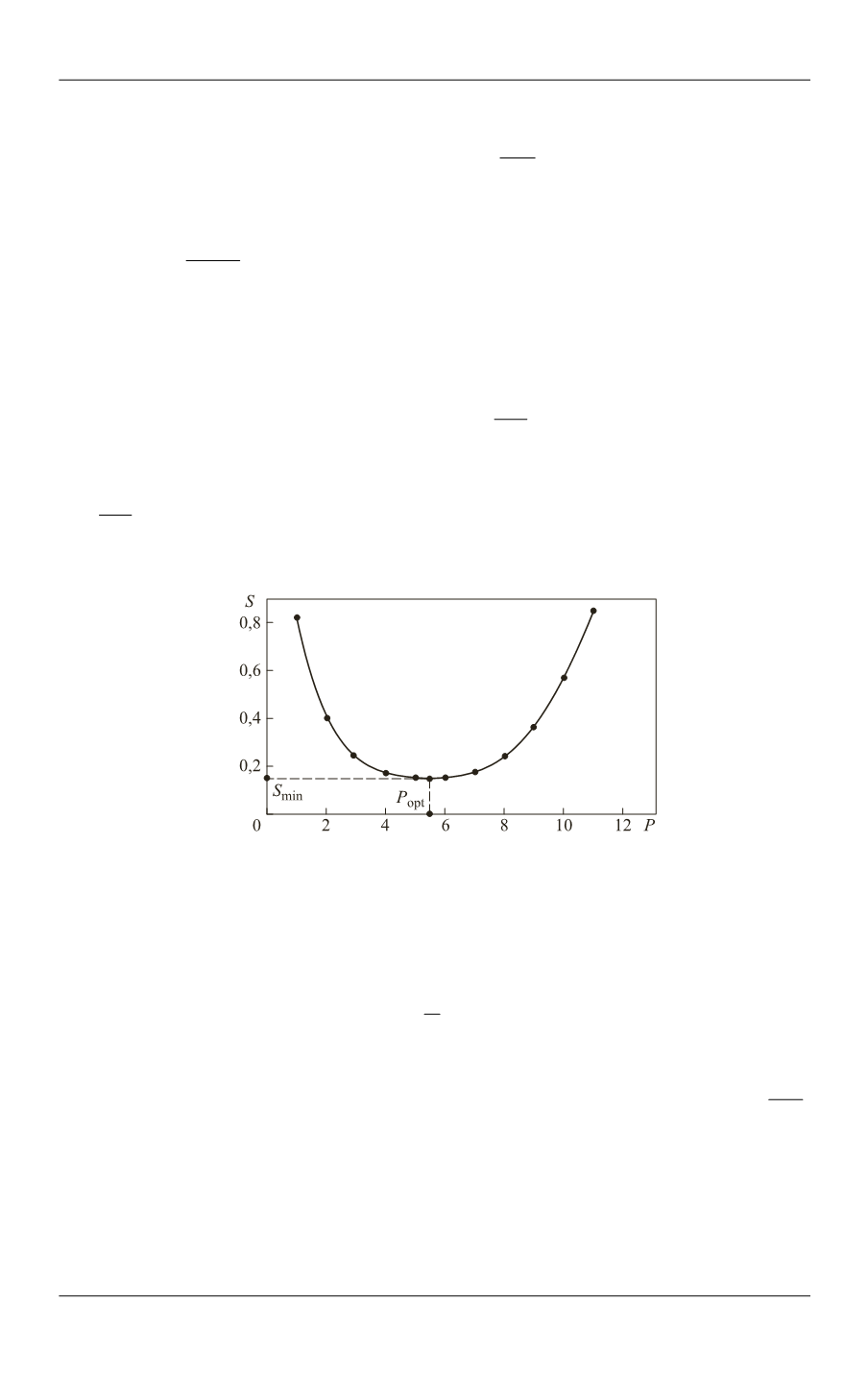
С.А. Тоноян, А.В. Балдин, Д.В. Елисеев
120
ISSN 0236-3933. Вестник МГТУ им. Н.Э. Баумана. Сер. Приборостроение. 2016. № 6
Проведя ранжирование по
,
m
e
определим точку
K
, для которой справедли-
во выражение:
k
e
= min
,
m
e
m
=
1, .
n
t
Модель, с помощью которой восстанавливается случайный процесс
,
i
X t
строится с помощью полиномов
j
-й степени по известным значениям
,
i
X t
i
=
1,
.
n k
Степень полинома определяется из условий
2
1
n k
i
j j
i
i
S
X t
a F t
= min,
(10)
где
i
X t
— исходный процесс, известный в интервале
1 1
,
;
n
T t t
j
i
F t
—
аппроксимирующий полином
j
-й степени,
j
=
1, .
P
Предположим, что зависимость
S f j
описывается кривой, показанной
на рис. 2. По формуле (10) вычисляется среднеквадратическое отклонение
S
при
j
=
1,
P
и определяется конкретное значение оптимальной степени аппрокси-
мирующего полинома или интервал ее нахождения (см. рис. 2).
Рис. 2.
Зависимость среднеквадратического отклонения
от сложности модели
Следующим этапом является определение адаптивных весовых коэффици-
ентов, удовлетворяющих условию
2
j
1
1
min,
n
i
j
j
i
i n k
U
X t
a F t
P
(11)
где
j
— адаптивные весовые коэффициенты, первоначально формируемые в
интервале обучения
0
1
1
,
,
n
n k
T t
t
а затем в интервале
2
1
,
,
n n l
T t
t
l
=
1, ,
m
т. е. в прогнозируемой области;
P
— степень аппроксимирующего полинома.
Суммы весовых коэффициентов должны удовлетворять условию
1
1.
P
j
j
(12)
















