В результате, каждый элемент матрицы
Т
будет иметь вид
t
[
i
] [
j
] = 2
i
x
+
X
2
q
mod
p,
где коэффициентом при
x
будет двойка в степени номера строки, а свободным
членом — некоторая сумма степеней двоек,
взятая по
модулю
р
.
В случае совпадения некоторых двух элементов в матрице
S
, их показа-
тели на соответствующих позициях в матрице
Т
также совпадут. Если это
будут элементы из разных строк, то коэффициенты при
x
будут различными.
Поэтому, приравняв эти элементы, мы получим уравнение вида
2
i
x
+
a
1
= 2
j
x
+
a
2
(
mod
p
)
(6)
с известными коэффициентами
a
1
и
a
2
. Если
a
1
6
=
a
2
, то уравнение (6)
будет иметь единственное, отличное от нуля решение. Тем самым, удастся
вычислить искомый показатель
x
.
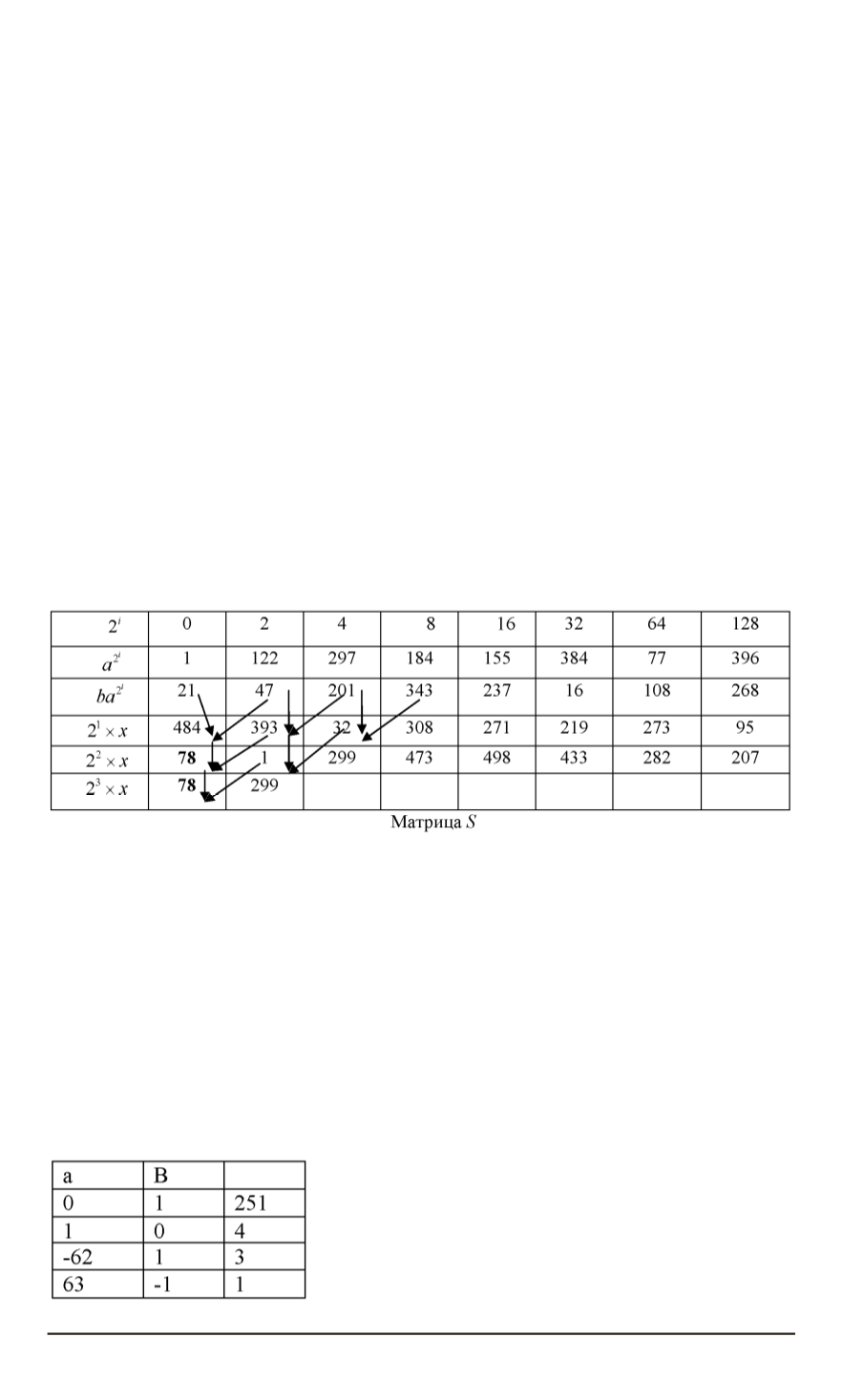
Пример.
В качестве примера рассмотрим циклическую группу по умно-
жению по модулю простого числа
p
= 503
. Вычислим дискретный логарифм
числа 318 по основанию 5.
p
−
1 = 502 = 2
•
251;
a
= 5
2
= 25;
b
= 318
2
= 21;
Для верхнего 78, соответствующий показатель равен:
2
2
x
+ (0 + 2) + (2 + 4)
mod
251
.
Показатель для 1:
2
2
x
+ (2 + 4) + (4 + 8)
mod
251
.
Для нижнего 78:
2
3
x
+ (0 + 2) + (2 + 4) + (2 + 4) + (4 + 8)
mod
251
.
Приравнивая показатели, получаем уравнение
2
2
x
+ 8 = 2
3
x
+ 26 (
mod
251)
,
4
x
= 233 (
mod
251)
.
По алгоритму Евклида
4
a
+ 251
b
= 1;
4
−
1
= 63 (
mod
251) ;
x
= 121 (
mod
251) ;
x
= ? (
mod
2) ;
т.к.
318
251
= 5
251
= 502
,
log
502
502 = 1
)
x
= 1 (
mod
2)
.
ISSN 0236-3933. Вестник МГТУ им. Н.Э. Баумана. Сер. “Приборостроение”. 2014. № 2 83


