Поэтому ответ:
log
5
318 =
x
= 121
.
Поскольку размер матрицы
S
невелик, возникает вопрос, всегда ли най-
дутся совпадающие элементы. Очевидно, что нет. Вычислим верхнюю гра-
ницу числа показателей
x
, для которых в матрице
S
всегда найдутся совпа-
дения. Для этого будем считать, что каждой паре элементов из матрицы
Т
соответствует уникальное уравнение, имеющее ненулевое решение, отлич-
ное от остальных (кроме пар, лежащих в одной строке). Общее число таких
пар
max =
N
(
N
−
1)
2
−
k
(
k
+ 1)
2
(
k
+ 1) =
N
2
,
(7)
N
= (
k
+ 1)
2
— число элементов в матрице
Т
. Таким образом, верхняя
граница показателей, для которых всегда найдется совпадение, соответствует
квадрату числа элементов в матрице, а число элементов в матрице — это число
умножений в группе, которые требуются для ее вычисления.
Чтобы оценить, насколько близко лежит реальное число показателей к
верхней границе, потребуется подсчитать число линейно зависимых уравне-
ний, которые дают одинаковые решения. Но сначала приведем результаты
экспериментов, в которых перебирались все пары и проводился подсчет уни-
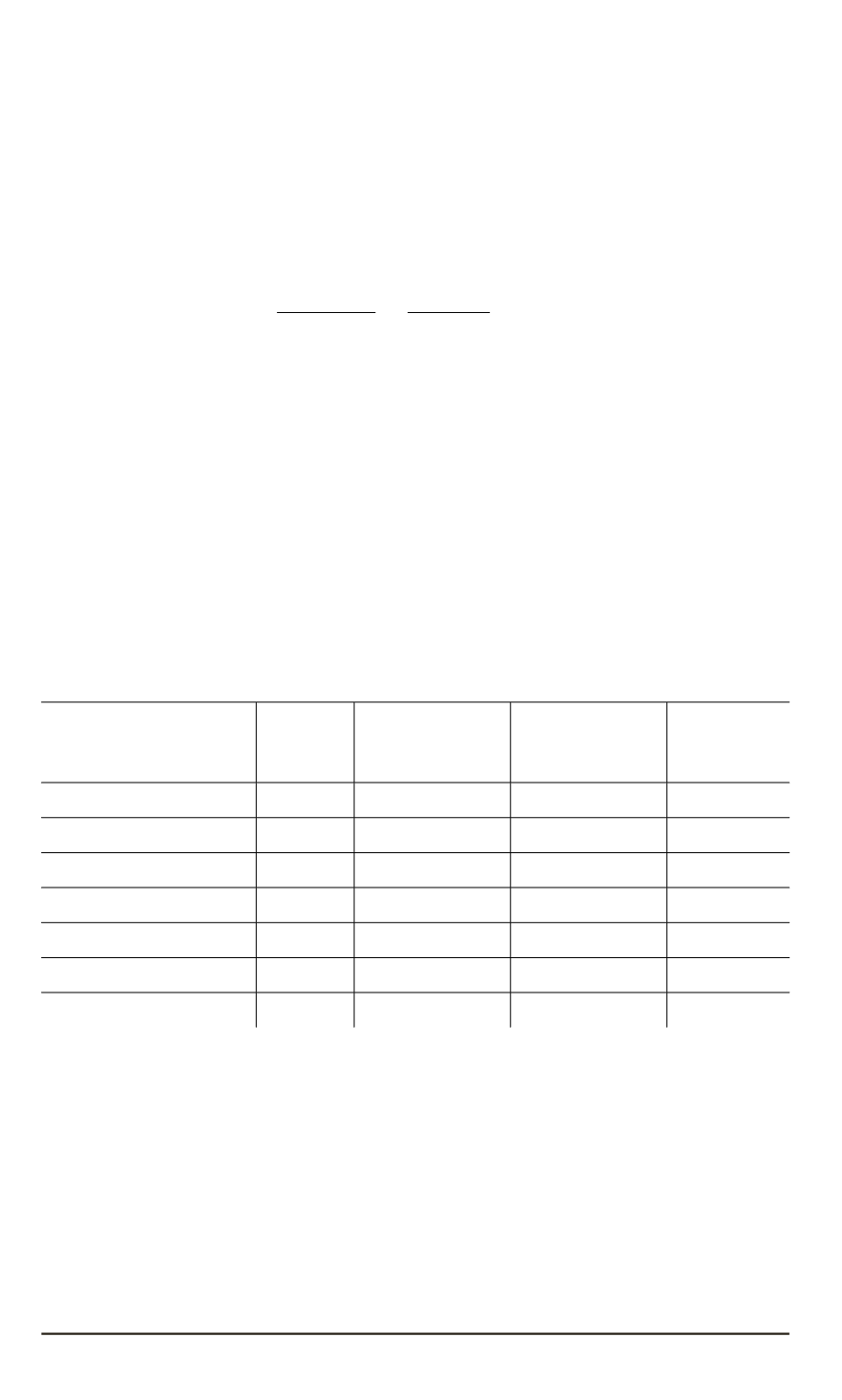
кальных решений. Эксперименты проводились для различных
р
(табл. 1).
Таблица 1
Эксперименты для двумерной матрицы
Простой модуль
k
= log
2
p
Число
различных
показателей
Верхняя
граница, (max)
Разность,
Δ
17 623
14
13 037
23 625
10 588
114 553
16
32 592
39 304
6 712
(
2
17
−
1
) 131 071
16
33 898
39 304
5 406
573 402 943
29
388 439
391 500
3 061
992 421 757
29
388 473
391 500
3 027
1 742 359 279
30
443 664
446 865
3 201
(
2
31
−
1
) 2 147 483 647 30
441 006
446 865
5 859
Разность
Δ
также была получена в ходе экспериментов, как число ре-
шений, которые совпадали с уже найденными, и полностью соответствует
значениям из табл. 1 (
Δ = max
минус число найденных различных пока-
зателей). Это очень важный момент, поскольку могли получиться решения,
равные нулю, которые не учитывались. Но оказалось, что их ни при каких
значениях
р
нет. Поэтому
Δ
— число линейно зависимых уравнений.
Теперь выполним теоретическую оценку. Линейный оператор отображе-
ния Ньютона (1) имеет квадратную матрицу следующего вида:
84 ISSN 0236-3933. Вестник МГТУ им. Н.Э. Баумана. Сер. “Приборостроение”. 2014. № 2


